
Bei der Kryptographie wird im Gegensatz zur Steganographie die geheim zu haltende Nachricht nicht versteckt. Sie ist als Nachricht erkennbar, kann aber von Unbefugten nicht erschlossen werden, weil nur unverständliche Zeichenfolgen zu sehen sind. Beim Absender der Nachricht gibt es ein Ver- und beim Empfänger ein Entschlüsselungsverfahren. In der Praxis stellt sich dies dem Benutzer oft als ein einziges Verfahren dar, vielleicht als Maschine (Hardware) realisiert, das wahlweise auf Ver- oder auf Entschlüsseln gestellt werden kann.
Die geheim zu haltenden Nachrichten liegen heutzutage in der Regel als Binärdateien auf einem Rechner vor. Früher waren es überwiegend Texte in einer natürlichen Sprache. Aus dieser Zeit stammen die Bezeichnungen Klartext für die ursprüngliche Nachricht und Geheimtext für das Ergebnis der Verschlüsselung. Beide Begriffe werden noch immer benutzt, und es ist lehrreich, die Verschlüsselungsverfahren an Texten einer natürlichen Sprache nachzuvollziehen. Deshalb wird im weiteren Verlauf der Betrachtungen so vorgegangen, als läge der Klartext als geschriebener Text der deutschen Sprache vor. In der Praxis werden selbstverständlich Binärdaten ver- und entschlüsselt und die hier vorgestellten Verfahren werden auf diese Daten übertragen.
Dem Vorgang der Ver- und Entschlüsselung (Chiffrierung und Dechiffrierung) liegt folgendes Modell zugrunde, das zeigt, dass das Ergebnis der Verschlüsselung eines Klartextes mithilfe eines Schlüssels ein Geheimtext ist, der wiederum durch die Entschlüsselung mithilfe eines Schlüssels zum ursprünglichen Klartext zurückführt:

Eng verbunden mit kryptographischen Verfahren, man spricht kurz von Kryptoverfahren, ist die Kryptoanalyse, die in der Literatur manchmal auch Kryptanalyse genannt wird. Darunter versteht man Techniken zum Entschlüsseln einer verschlüsselten Nachricht ohne Kenntnis des Schlüssels. Sprachwissenschaftliche (linguistische) und mathematische Verfahren sind das Handwerkszeug der Kryptoanalytiker. Einrichtungen, in denen Kryptoanalyse betrieben wird, gibt es in allen Ländern. Bekannt ist die NSA (National Security Agency) der Vereinigten Staaten von Amerika.
Die Konsequenzen des Brechens von Verschlüsselungen sind manchmal dramatisch. So geht das Todesurteil gegen Maria Stuart (vollstreckt 1587) auf das Brechen einer Verschlüsselung zurück. Dadurch wurde der Nachweis einer Verstrickung in eine Intrige gegen die englische Königin erbracht.
Die Betrachtung kryptoanalytischer Techniken, so fachlich anspruchsvoll diese auch sind, ist nicht Gegenstand einer Lehrveranstaltung über verteilte Systeme und wird deshalb hier nicht weiter verfolgt.
Wird sowohl für das Ver- als auch für das Entschlüsseln der gleiche Schlüssel verwendet, dann wird das zugehörige kryptographische Verfahren symmetrisch genannt. Über viele Jahrtausende hinweg war es unvorstellbar, dass es kryptographische Verfahren geben könnte, die für die Chiffrierung und Dechiffrierung zwei verschiedene Schlüssel verwenden. Erst am Ende der siebziger Jahre des vorigen Jahrhunderts wurden solche asymmetrischen Verfahren gefunden und praktisch eingesetzt. Bevor sie in ihrer prinzipiellen Arbeitsweise vorgestellt werden, soll kurz auf die historisch älteren symmetrischen Verfahren eingegangen werden.
Um einen Text unleserlich zu machen, können die einzelnen Zeichen oder Zeichenketten des Textes durch andere Zeichen oder Zeichenketten ersetzt werden, die möglicherweise den gleichen Zeichenvorrat verwenden, wie der Text selbst. Ist Letzteres der Fall, dann spricht man von einer monoalphabetischen Substitution. Alternativ zum Ersetzen von Zeichen oder Zeichenfolgen können diese in ihrer Position im Text verändert werden. Und beide Vorgehensweisen können miteinander kombiniert werden.
Ein sehr einfaches Zeichenersetzungsverfahren ist nach dem römischen Kaiser Gaius Julius Cäsar (100-44 v.C.) benannt. Bei ihm wird jedes Zeichen des Klartextes durch das (zyklisch) n-nächste Zeichen im Alphabet ersetzt. Die Zahl n ist der Schlüssel des Verfahrens. Ist n gleich 0, bleibt der Klartext unverändert, bei n gleich 1 wird a duch b ersetzt usw. Bei diesem elementaren Verfahren sind sowohl das Entschlüsselungsverfahren als auch die Schlüsselsymmetrie gut zu erkennen.
Eine ebenfalls sehr elementare Positionsvertauschung ist das Rückwärtsschreiben von Textstücken fester Länge. Der Schlüssel ist hier die Länge der Textstücke. Und auch in diesem Fall sind das Entschlüsselungsverfahren und die Schlüsselsymmetrie deutlich zu sehen.
Bereits im 16. Jahrhundert wurde ein Zeichenersetzungsverfahren entwickelt (Blaise de Vigenère, 1585), bei dem jedes einzelne Zeichen eines Klartextes mit einem anderen Schlüssel verschlüsselt wird. Dadurch wird ein bestimmtes Zeichen des Klartextalphabets, wie beispielsweise der Buchstabe e der deutschen Sprache, bei jedem Auftreten im Klartext anders verschlüsselt. Die auf deutscher Seite im 2. Weltkrieg eingesetzte Verschlüsselungsmaschine Enigma realisiert eine Vigenère-Verschlüsselung mit einem Schlüsselraum aus etwa 1017 Schlüsseln.
Der amerikanische Mathematiker und Begründer der Informationstheorie Claude Shannon bewies 1949, dass dieses Verfahren, wenn
nicht gebrochen werden kann. Man spricht dann von einem One Time Pad. Sein praktischer Nachteil ist die Länge der Schlüsselfolge. Dennoch gibt es nach wie vor Anwendungen für dieses Verfahren, vorallem in der Diplomatie. Nachweislich wurde es im Nachrichtenverkehr zwischen Fidel Castro und Che Guevara eingesetzt.
Wird ein Klartext Zeichen für Zeichen verschlüsselt, spricht man von einer Stromchiffrierung oder kurz von einer Stromchiffre. Bei einer Blockchiffre wird der Klartext in Textblöcke mit einer fest vorgegebenen Länge eingeteilt. Der letzte Block muss gegebenenfalls mit zufällig gewählten Zeichen aufgefüllt werden. Jeder Klartextblock wird unabhängig von allen anderen Blöcken verschlüsselt und in einen Geheimtextblock überführt, wobei auch die Geheimtextblöcke alle die gleiche Länge haben. Jede Blockverschlüsselung ist eine Folge von Zeichenersetzungen und Halbblockvertauschungen.
Weite Verbreitung hat eine Blockchiffre namens Data Encryption Standard (DES) gefunden. Sie wurde 1977 vom IBM-Konzern vorgestellt und von der amerikanischen National Security Agency (NSA) als Standard übernommen. Das Verfahren arbeitet mit einer Blockgröße von 64 Bit und einer Schlüssellänge von ebenfalls 64 Bit. Jeder Klartextblock wird zunächst in zwei gleich große Halbblöcke (anschaulich in einen linken und einen rechten) zerlegt. Aus dem Schlüssel werden 16 über Bits operierende sogenannte Teilschlüssel, das sind Zeichenersetzungsfunktionen, fn() (n=1,...,16) abgeleitet und folgendermaßen eingesetzt:
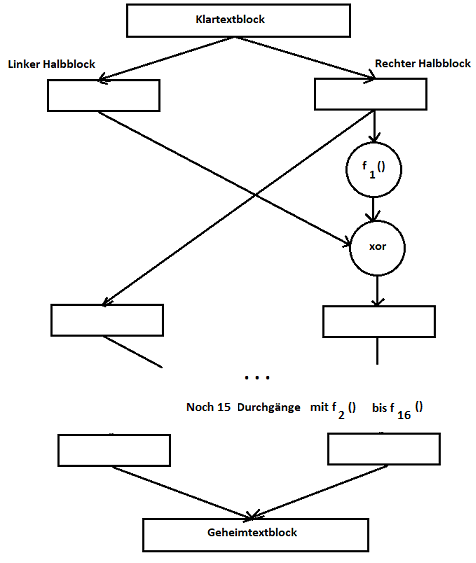
Eine Weiterentwicklung des DES wurde notwendig, nachdem es 1994 erstmal gelang, die Chiffre zu brechen. Der daraus hervorgegangene Advanced Data Encryptiom Standard (AES) ist ebenfalls eine Blockchiffre und im Jahre 2000 von der NSA übernommen worden. Das Verfahren verwendet eine Blocklänge von 128 Bit und erlaubt Schlüssellängen von 128, 192 und 256 Bit. Hier bestimmt die Schlüssellänge die Anzahl an Halbblockoperationen. Es sind 10, 12 bzw. 14 Durchgänge. Mit Schlüssellängen von 192 und 256 Bit ist der AES in den Regierungsbehörden der USA für Dokumente mit höchster Geheimhaltungsstufe zugelassen.
Über Jahrhunderte hinweg waren in der Kryptographie nur symmetrische Verschlüsselungsverfahren bekannt, und es war unumstritten, dass der Schlüssel, den Absender und Empfänger gleichermaßen benutzen, irgendwie zwischen ihnen abgesprochen, zwischen ihnen transportiert oder ihnen beiden von dritter Seite zugestellt werden muss. Hat nicht vorab eine Schlüsselabsprache stattgefunden, dann ist ein Schlüsseltransport unabdingbar. Dass dies nicht richtig ist, wurde um das Jahr 1975 herum entdeckt, als in der Mathematik damit begonnen wurde, spezielle Sachverhalte aus der Zahlentheorie in der Kryptographie anzuwenden. Benutzt werden mathematische Funktionen (Abbildungen) f(), die über natürlichen Zahlen operieren und die Eigenschaft haben, dass es
Ein bekanntes Beispiel für eine solche Funktion stellt die Multiplikation zweier Primzahlen dar, denn
Derartige Funktionen werden One Way Functions, im Deutschen meist Falltürfunktionen oder Einbahnstraßenfunktionen genannt. Die Falltüreigenschaft kommt daher, dass bislang keine Formel bekannt ist, mit der aus einer natürlichen Zahl einer ihrer Primfaktoren berechnet werden kann. Es bleibt nur die Methode, systematisch alle Primzahlen durchzuprobieren, bis der kleinste Faktor gefunden ist. Das Raffinierte an den One Way Functions ist der Sachverhalt, dass man das Verfahren kennt, um zum Ziel zu kommen, bei sehr großen Zahlen der Rechenaufwand jedoch zu hoch ist, um es praktisch erreichen zu können. Der Begriff der Sicherheit eines Kryptoverfahrens wird damit auf den Arbeitsaufwand für eine Berechnung zurückgeführt.
1976 veröffentlichten die amerikanischen Mathematiker Whitfield Diffie und Martin Hellman ein mit einer One Way Function arbeitendes Schlüsselaustauschverfahren, das ohne einen expliziten Schlüssseltransport auskommt. Ausgangspunkt dabei ist die Überlegung, dass jeder Schlüssel eine Zeichenkette ist, die durch ihre Binärdarstellung in einem Rechner als natürliche Zahl betrachtet werden kann. Das Verfahren von Diffie und Hellman bewirkt, dass Sender und Empfänger die gleiche Zahl zum Ver- bzw. zum Entschlüsseln berechnen.
Benutzt wird die Potenzierung natürlicher Zahlen verbunden mit einer Modulorechnung, die in der Schulmathematik häufig als Uhrenarithmetik bezeichnet wird, weil eine Zeigeruhr sehr anschaulich die Arbeitsweise dieses Rechnens zeigt. Diffie und Hellman benutzten die Funktion
f(x) = gx mod p, wobei p prim und g < p ist.Zu y = gx gehört die Umkehrfunktion x = logg(y). Aber durch die Modulorechnung gibt es auch hier keine Formel, um zu einem Funktionswert den Ursprungswert zu berechnen. Es bleibt nur das Durchprobieren von x-Werten.
Die folgende Beschreibung des Verfahrens von Diffie und Hellman geht von einer Situation aus, bei der ein Absender A einem Empfänger B eine verschlüsselte Nachricht zukommen lassen will, die von einer dritten (feindlich handelnden) Person E mitgelesen wird. Bei der anschaulichen Beschreibung kryptographischer Verfahren ist es weit verbreitet, Namen für die handelnden Parteien zu vergeben. Absenderin A heißt üblicherweise Alice, Empfänger B Bob und die dritte Person E Eve (in Anlehnung an die englische Bezeichnung eavesdropper, was auf deutsch Lauscher(in) oder Horcher(in) bedeutet). Vorgegangen wird folgendermaßen:
Alice und Bob verfügen nach ihren Berechnungen über den gleichen Schlüssel, ohne dass dieser explizit transportiert werden musste, und Eve kennt alle übertragenen Zahlen und ihre Bedeutung. Aber sie hat keine Formel, um den Wert a aus A oder b aus B zu berechnen, so dass ihr nur die Möglichkeit bleibt, a- oder b-Werte durchzuprobieren, was bei ausreichend großem p unakzeptabel lange dauert.
Nachdem Diffie und Hellman gezeigt hatten, wie über einen unsicheren Kanal ein gemeinsamer Schlüssel vereinbart werden kann, entwickelten Mathematiker Verschlüsselungsverfahren mit zwei Schlüsseln, von denen einer geheim gehalten und der andere an den Partner übermittelt wird. Der Erstere der beiden heißt privater oder geheimer, der andere öffentlicher Schlüssel. Kryptoverfahren, die darauf beruhen, werden meist Public-Key-Systeme oder asymmetrische Verschlüsselungsverfahren genannt.
Das wohl bekannteste Public-Key-System wurde 1979 von den amerikanischen Mathematikern Ronald L. Rivest, Adi Shamir und Leonard Adleman vorgestellt. Nach den Anfangsbuchstaben ihrer Namen wird es als RSA-Verfahren bezeichnet. Es realisiert eine monoalphabetische Zeichenersetzung. Die folgende Beschreibung seiner Funktionsweise ist bewusst grob und mathematisch ungenau gehalten. Eine mathematisch korrekte Darstellung würde eine doch recht umfangreiche Beschäftigung mit Teilen der Zahlentheorie voraussetzen und an den Inhalten einer Lehrveranstaltung über verteilte Systeme vorbeigehen.
Bei einem Public-Key-System gibt es ein Verschlüsselungsverfahren f(), das durch die beiden Parameter Klartext K und erster Schlüssel s1 gesteuert wird. Dazu gehört ein Entschlüsselungsverfahren g(), das mit den Parametern Geheimtext G und zweiter Schlüssel s2 arbeitet. f(), g(), s1 und s2 sind so angelegt, dass gilt:
Die beiden Schlüssel s1 und s2 sind gleichberechtigt. Jeder von ihnen kann von seinem Erzeuger als öffentlicher bzw. als geheimer (geheimzuhaltender) Schlüssel verwendet werden. In der Praxis wird für eine Schlüsselpaarerzeugung ein Programm verwendet, das üblicherweise festlegt, welcher der beiden Schlüssel wofür zu verwenden ist.
Wie bereits bei der Beschreibung des Diffie/Hellman-Verfahrens werden im Folgenden die beteiligten Parteien mit den Namen Alice als Senderin, Bob als Empfänger und Eve als Lauscherin bezeichnet. Vorausgesetzt, dass Alice und Bob ein und dasselbe Public-Key-System verwenden, läuft das Verfahren im Prinzip folgendermaßen ab:
Eine Lauscherin Eve hat sowohl Bobs öffentlichen Schlüssel als auch den Geheimtext erfahren, kann jedoch nicht in akzeptabler Zeit daraus Bobs geheimen Schlüssel berechnen, den sie aber zum Entschlüsseln des Geheimtextes bräuchte.
Asymmetrische Verschlüsselungsverfahren sind rechenintensiv und dadurch deutlich langsamer als symmetrische Verfahren. Deshalb spielen symmetrische Verfahren in der praktischen Kryptographie immer noch eine wichtige Rolle. Häufig findet man gemischte Verfahren, bei denen ein Klartext mit einem symmetrischen, der zugehörige Schlüssel jedoch mit einem asymmetrischen Verfahren verschlüsselt wird, was das Problem des Schlüsseltransports symmetrischer Verfahren löst.
Ein solches gemischtes System namens Pretty Good Privacy (PGP ) hat 1991 der amerikanische Softwareentwickler Phil Zimmermann für das Verschlüsseln von E-Mails entwickelt. Es ist frei verfügbar und auf vielen Rechner-Plattformen implementiert. Durch sein Vorgehen hat er sich Schwierigkeiten mit der amerikanischen Zollbehörde eingehandelt. PGP verschlüsselt E-Mails mit einem AES-ähnlichen Verfahren und den Schlüssel mit RSA.
Die Übermittlung eines digitalen Dokuments, wie zum Beispiel eines öffentlichen Schlüssels bei der Verwendung eines asymmetrischen Verschlüsselungsverfahrens, wirft die Frage nach der Authentizität dieses Dokuments auf. Um beim Beispiel eines asymmetrischen Verfahrens zu bleiben: Wenn die Lauscherin Eve nicht nur Lauschen, sondern sich aktiv an der Kommunikation zwischen Alice und Bob beteiligen kann, dann könnte sie ein eigenes Schlüsselpaar erzeugen und Alice gegenüber vorgeben Bob zu sein, während sie Bob gegenüber vorgibt Alice zu sein. Da bei digitalen Dokumenten die handschriftliche Unterzeichnung fehlt, entsteht ein Authentifizierungsproblem.
Um sicher zu sein, das richtige digitale Dokument erhalten zu haben, könnte der Empfänger sich beispielsweise das Dokument mehrfach und auf jeweils anderen Wegen holen und dann die empfangenen Dokumente miteinander vergleichen. Das wäre allerdings ein sehr aufwändiges Vorgehen. Interessanterweise bietet die asymmetrische Verschlüsselung eine Lösung für das Authentifizierungsproblem. Bevor das Verfahren beschrieben wird, muss kurz auf den Begriff des digitalen Fingerabdrucks eingegangen werden.
Hintergrund sind sogenannte Hashfunktionen. Das sind mathematische Funktionen, die aus einer Zeichenkette eine natürliche Zahl berechnen, die üblicherweise eine feste Länge hat. Diese Zahl wird als Hashwert oder Hashcode der Zeichenkette bezeichnet.
Als (sehr) elementares Beispiel betrachte man eine Funktion, für die Folgendes festgelegt wird:
Diese Funktion berechnet aus der Zeichenkette ABBA durch Zuordnung der Zahlen für die einzelnen Zeichen zunächst die Zahlenfolge 1, 2, 2, 1 und daraus die Quersumme 6. Offensichtlich ist diese Hashfunktion als digitaler Fingerabdruck unbrauchbar, weil viel zu viele Zeichenfolgen zu dem gleichen Hashwert führen. Man spricht von einer Vielzahl von Kollisionen.
Für einen digitaler Fingerabdruck können nur Hashfunktionen verwendet werden, die sehr empfindlich auf jede Veränderung der zugrunde liegenden Zeichenkette reagieren und bei denen nur sehr wenige Kollisionen auftreten. Im Laufe der Jahre sind viele derartige Hashfunktionen gefunden worden. Sie werden als kryptographische Hashfunktionen bezeichnet. Die bekanntesten davon sind wohl
Bei der Erstellung einer digitalen Signatur (eines digitalen Fingerabdrucks) ist anders vorzugehen als beim Verschlüsseln von Dokumenten, denn jetzt erzeugt nicht der spätere Empfänger eines Dokuments ein Schlüsselpaar (sg, so) mit einem geheimen und einem öffentlichen Schlüssel, sondern der Sender. Um den Ablauf zu beschreiben, werden wieder die Namen Alice für die Senderin und Bob für den Empfänger benutzt, und es wird vorausgesetzt, dass Alice und Bob ein und dasselbe Public-Key-System und ein und dieselbe kryptographische Hashfunktion verwenden.
Eine Lauscherin Eve, die Kenntnis über D, sig und so erlangt hat, kann nichts ausrichten, weil ihr der geheime Schlüssel von Alice fehlt und sie diesen nicht in akzeptabler Zeit aus dem öffentlichen Schlüssel berechnen kann.
In den letzten Jahren wird immer wieder über Fortschritte im Bereich der Quantenkryptographie berichtet. Das ist nach wie vor ein Forschungsgegenstand, der allerdings auf einen praktischen Einsatz zusteuert. Da er diesen noch nicht erreicht hat, sollen hier einige wenige Bemerkungen zu diesem Thema genügen.
Unserer menschlichen Erfahrung nach kann man etwas betrachten, ohne dadurch an dem Betrachteten Spuren zu hinterlassen. Beispielsweise kann man ein Schriftstück lesen, ohne dass danach diesem Schriftstück angesehen werden kann, dass es gelesen worden ist. In der Welt der Quanten, das ist die Welt des sehr, sehr Kleinen, ist das anders. Es ist nicht möglich, ein Quantenobjekt wie z.B. ein Photon (Lichtteilchen) zu beobachten, ohne dadurch auf es einzuwirken. Die Beobachtung, auch die indirekte, verändert das beobachtete Objekt, wodurch ein wie auch immer geartetes Abhören sofort entdeckt werden kann. Das ist der Hintergrund der Quantenkryptographie.
Bereits 1984 haben der amerikanische Physiker und Informatiker Charles, Henry Bennet und der kanadische Informatiker und theoretische Physiker Gilles Brassard ein Verfahren für einen sicheren Schlüsseltransport vorgeschlagen, bei dem Licht, mit dessen Polarisation Bits kodiert werden, als Informationsträger verwendet wird. Bei den ersten Versuchen war der Übertragungsweg in einem Glasfaserkabel nur 30 cm lang. Inzwischen werden schon viele Kilometer erreicht und es gibt bereits kabelungebundene (Freiluft-) Übertragungen.