Eine Blockchain setzt als Hilfsmittel unter anderem zwei mathematische Konzepte ein, die beide der Kryptographie zuzuordnen sind. Bei dem einen ist diese Zuordnung mehr peripher, bei dem anderen zentral. Mehr peripher für die Kryptographie ist das Konzept der Hashfunktion, zentral dagegen das der asymmetrischen Verschlüsselung. Zunächst soll hier auf Hashfunktionen eingegangen werden.
Durch eine Hashfunktion wird einer Zeichenkette (einem String) eine natürliche Zahl zugeordnet. Die Zahl heißt Hashcode oder Hashwert der Zeichenkette. Es ist möglich, die Zuordnung injektiv zu gestalten, was bedeutet, dass zwei verschiedenen Zeichenketten immer zwei verschiedene Hashwerte zugeordnet werden. Allerdings führen derartige Funktionen zu sehr großen Zahlen. Diese haben einen so riesigen Speicherbedarf und erfordern so lange Bearbeitungszeiten, dass mit ihnen in der Praxis nicht gearbeitet wird. Das heißt, dass praktisch eingesetzte Hashfunktionen nicht injektiv sind. Bei ihnen können sogenannte Kollisionen auftreten, also Situationen, in denen zwei verschiedenen Zeichenketten ein und derselbe Hashwert zugeordnet wird. Solche Situationen müssen dann abhängig von der konkreten Anwendung behandelt werden.
Als sehr elementares Beispiel einer Hashfunktion betrachte man die folgendes Zuordnung von Zeichenketten zu natürlichen Zahlen:
Diese Funktion berechnet beispielsweise aus der Zeichenkette ABBA durch Zuordnung der Zahlen für die einzelnen Zeichen zunächst die Zahlenfolge 1, 2, 2, 1 und daraus die Quersumme 6. Ob diese Hashfunktion überhaupt eine praktische Anwendung hat, sei dahingestellt. Mit Sicherheit ist sie ungeeignet einen Datenbestand, zum Beispiel ein Schriftstück, zu identifizieren. Sie kann wegen ihrer Vielzahl an Kollisionen nicht als digitaler Fingerabdruck verwendet werden. Beispielsweise führen unter anderem die folgende Zeichenketten alle zu dem Hashwert 6:
Als zweites Beispiel soll eine Hashfunktion vorgestellt werden, die extrem empfindlich auf jede Veränderung der zugrunde liegenden Zeichenkette reagiert. Wie beim ersten Beispiel wird zunächst jedem Zeichen des gegebenen Zeichenvorrats eine natürliche Zahl zugeordnet, zum Beispiel wieder so, dass das Zeichen A die Zahl 1 erhält, das Zeichen B die Zahl 2 usw. Dann wird in dem String, dessen Hashwert berechnet werden soll, jedem Zeichen seine Position, gezählt von links nach rechts, zugeordnet. Als Positionsnummer wird dabei jedoch nicht die Folge der natürlichen Zahlen, sondern die Folge der Primzahlen (2, 3, 5, 7, 11, ...) verwendet. Zu dem String ABBA beispielsweise gehört dann die folgende Positionsfolge:
Um den Hashwert eines Strings zu berechnen, wird in zwei Schritten ein Produkt aus Potenzen gebildet. Zuerst wird das Produkt aus Positionsnummer hoch zugehörigem Zeichen notiert. Im Beispiel ABBA entsteht das folgende Gebilde:
Im zweiten Schritt werden die Zeichen des Strings in diesem Ausdruck durch die ihnen anfangs zugeordneten Zahlen ersetzt. In Fortführung des Beispiels ergibt sich:
Wird diese Hashfunktion h() genannt, dann liefert sie den Hashwert:
Im Vergleich mit dem ersten Beispiel berechnet diese Funktion bei den gleichen Zeichenfolgen wie dort jetzt folgende Hashwerte:
Die zweite Hashfunktion zeigt jede - auch die geringste - Veränderung eines Strings an! Leider führt sie mit zunehmender Stringlänge zu kaum noch oder gar nicht mehr handhabbaren riesigen Zahlen. An eine Hashfunktion, die in der Praxis eingesetzt werden soll, werden eine ganze Reihe von Anforderungen gestellt. Dazu gehören insbesondere die folgenden:
Funktionen, die diese Anforderungen erfüllen, werden als kryptographische Hashfunktionen bezeichnet. Im Laufe der Jahre sind eine ganze Reihe von ihnen gefunden worden. Weit verbreitet sind die folgenden, die alle so gestaltet worden sind, dass sie Zeichenketten auf natürliche Zahlen fester Länge abbilden, die sie gegebenenfalls mit führenden Nullen belegen.
Mit dem Begriff digitaler Fingerabdruck ist bereits eine Anwendung von kryptographischen Hashfunktionen genannt worden. Allgemeiner betrachtet werden diese Funktionen in der Praxis verwendet, um
Bei den ersten beiden Anwendungen wird ausgenutzt, dass zwei identische Datenbestände, gleich welcher Art sie auch sein mögen (es könnte sich um zwei Schriftstücke handeln), bei ein und derselben kryptographischen Hashfunktion mit großer Wahrscheinlichkeit den gleichen Hashwert erhalten. (Die Einschränkung entsteht durch die nur beinahe vorhandene Injektivität der Funktion.) Das heißt, dass mit kryotographischen Hashfunktionen und unter Beachtung der Einschränkung ein Datenbestand identifiziert werden kann. Der Hashwert kann damit als digitaler Fingerabdruck dienen.
Nicht ganz so offensichtlich sind die letzten beiden der genannten Anwendungen. Von einer Hashreferenz spricht man, wenn der Hashwert einer Zeichenkette direkt oder indirekt als die Adresse einer Speicherstelle benutzt wird, an der die Zeichenkette abgelegt wird. Im Datenbankbereich beispielsweise kann man zu einem Datensatz den Hashwert der Zeichenkette bilden, die der Attributkombination des Primärschlüssels entspricht, und den gesamten Datensatz an der sich daraus ergebenden Adresse ablegen. Damit kann über den Primärschlüssel mithilfe der Hashfunktion schnell auf den Datensatz zugegriffen werden.
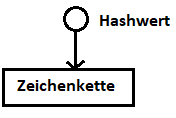
Durch diesen Zugriff auf eine Zeichenkette über ihren Hashwert kann dieser als eine Referenz (eine Art Zeiger) auf die Zeichenkette aufgefasst werden. Anschaulich ergibt sich folgendes Bild:

Wird der Hashwert einer Zeichenkette selbst wieder als Zeichenkette dargestellt, dann kann von diesem Hashwert ebenfalls der Hashwert bestimmt werden. Dadurch ergibt sich eine Referenz auf eine Referenz:
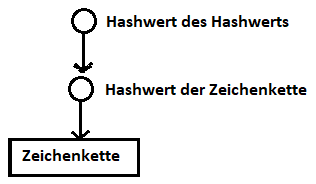
Eine Blockchain macht regen Gebrauch von Hashreferenzen. Darauf wird in den beiden folgenden Abschnitten 8.4.3 (Blöcke) und 8.4.4 (Ketten) noch näher eingegangen.
Auch die letzte der genannten Anwendungen spielt in Blockchains, die dem Nakamoto-Ansatz folgen, eine wichtige Rolle. Sie beschreibt die Wirkungsweise eines sogenannten Proof of Work, was ins Deutsche meist als Arbeitsnachweis übertragen wird. Dabei geht es darum, einen Teilnehmer (eine Person oder einen Prozess auf einem Rechner) am Betrieb eines bestimmten Systems eine zeitlang von seiner Teilnahme abzuhalten. Ein solcher Proof of Work ist bereits im Zusammenhang mit dem massenhaften Versenden von Spam-E-Mails diskutiert worden. Wenn man es so einrichtet, dass nach dem Versenden einer E-Mail der Sender ein bisschen warten muss, bevor er die nächste E-Mail senden kann, dann dauert das Versenden von einer Million E-Mails bei einer Wartezeit von jeweils 30 Sekunden bereits mehrere Tage.
Mit kryptologischen Hashfunktionen ist ein Proof of Work durch das Stellen eines sogenannten Hashpuzzles realisierbar. Das ist eine Aufgabe, die darin besteht, dass der den Arbeitsnachweis Erbringende eine vorgegebene Zeichenkette so verlängern muss, dass der Hashwert der durch die Verlängerung entstandenen Zeichenkette eine bestimmte Bedingung erfüllt. Beispielsweise lautet bei der von Nakamoto konzipierten Blockchain die Bedingung, dass der Hashwert mit einer bestimmten Zahl von Nullen beginnen muss. Die zu findende Ergänzung der vorgegebenen Zeichenkette wird Nonce genannt. Das ist eine Verkürzung des Ausdrucks Number (used) once und steht für eine Zeichenkette, also nicht nur für eine Zahl, die nur zu einem einmaligen Gebrauch vorgesehen ist.
Dass eine solche Aufgabenstellung als Proof of Work dienen kann, kommt daher, weil es aufgrund der Falltüreigenschaft einer kryptographischen Hashfunktion nicht möglich ist, in akzeptabler Zeit einen Nonce zu finden. Da es dafür keine Formel gibt, bleibt nur das Durchprobieren von Zeichenketten. Das Überprüfen eines angeblichen Nonce dagegen kann sehr schnell durchgeführt werden. Für die von Nakamoto verwendete Hashbedingung gilt übrigens, dass das Suchen eines Nonce umso länger dauert, je mehr führende Nullen beim Hashwert gefordert werden. Die Anzahl der führenden Nullen wird bei diesem Verfahren als Schwierigkeitsgrad des Hashpuzzles bezeichnet.
Die klassische Kryptographie hat die Aufgabe, Daten - egal welcher Art sie auch sein mögen - vor einem direkten oder indirekten Zugriff durch unberechtigte Personen zu schützen. Mit der asymmetrischen Kryptographie ist eine weitere Aufgabe hinzugekommen: Mit ihr können digitale Unterschriften geleistet werden. In diesem die Lehrveranstaltung verteilte Systeme ergänzenden Kapitel über Blockchain-Konzepte kann auf das Fachgebiet Kryptologie, zu dem die Kryptographie gehört, nur sehr rudimentär eingegangen werden.
Der niederländische Kryptologe Auguste Kerckhoffs formulierte im Jahr 1833 in militärischen Schriften eine Maxime für die Entwicklung kryptologischer Verfahren, die bis heute Bestand hat. Sie verlangt, dass die Sicherheit eines kryptologischen Systems nicht von der Geheimhaltung des Verschlüsselungsverfahrens abhängen darf, sondern nur von frei wählbaren Eingangsgrößen. Diese Eingangsgrößen werden als Schlüssel bezeichnet. Kerckhoffs' Prinzip verlangt, dass es ohne Kenntnis des Schlüssels nicht möglich sein darf, eine verschlüsselte Nachricht zu entziffern. Die Anzahl der möglichen Schlüssel zu einem kryptologischen Verfahren, der sogenannte Schlüsselraum, muss deshalb so groß sein, dass Rateversuche unakzeptabel lange dauern.
Die geheim zu haltenden Nachrichten liegen heutzutage in der Regel als Binärdateien auf einem Rechner vor. Früher waren es überwiegend Texte in einer natürlichen Sprache. Aus dieser Zeit stammen die Bezeichnungen Klartext für die ursprüngliche Nachricht und Geheimtext für das Ergebnis der Verschlüsselung. Beide Begriffe werden noch immer benutzt. Deshalb wird im weiteren Verlauf der Betrachtungen so vorgegangen, als läge der Klartext als geschriebener Text der deutschen Sprache vor. In der Praxis werden selbstverständlich Binärdaten ver- und entschlüsselt und die hier vorgestellten Verfahren werden auf diese Daten übertragen.
Dem Vorgang einer Ver- und Entschlüsselung (Chiffrierung und Dechiffrierung) liegt folgendes Datenflussmodell zugrunde:

Wird sowohl für das Ver- als auch für das Entschlüsseln der gleiche Schlüssel verwendet, dann wird das zugehörige kryptographische Verfahren symmetrisch genannt. Ein bekanntes und weit verbreitetes symmetrisches Verschlüsselungsverfahren ist der Advanced Data Encryptiom Standard (AES), der im Jahre 2000 von der amerikanischen Sicherheitsbehörde National Security Agency (NSA) übernommen wurde. Über viele Jahrtausende hinweg war es unvorstellbar, dass es kryptographische Verfahren geben könnte, die für die Chiffrierung und Dechiffrierung zwei verschiedene Schlüssel verwenden. Erst am Ende der siebziger Jahre des vorigen Jahrhunderts wurden solche asymmetrischen Verfahren gefunden und praktisch eingesetzt. In den folgenden Abschnitten werden symmetrische Verschlüsselungsverfahren aus Zeitgründen nicht weiter behandelt. Interessierte seien auf das Buch von F.L. Bauer verwiesen:

Etwa im Jahr 1975 wurde entdeckt, dass es möglich ist, kryptographische Verfahren zu entwickeln, bei denen für die Verschlüsselung ein anderer Schlüssel verwendet wird als für die Entschlüsselung. Dazu werden mathematische Funktionen herangezogen, die wie die kryptologischen Hashfunktionen Falltürfunktionen sind. Mit ihnen kann ein Schlüsselpaar erzeugt werden, dessen beide Schlüssel miteinander verwoben sind. Durch die Falltüreigenschaft der erzeugenden Funktion ist es praktisch nicht möglich, den einen der beiden Schlüssel aus dem jeweils anderen zu berechnen. Einer der beiden Schlüssel wird geheim gehalten und der andere öffentlich gemacht. Der geheim gehaltene Schlüssel wird üblicherweise geheimer oder privater, der andere öffentlicher Schlüssel genannt. Kryptographische Verfahren, die auf diese Weise arbeiten, werden meist Public-Key-Systeme oder asymmetrische Verschlüsselungsverfahren genannt. Das wohl bekannteste Public-Key-System wurde 1979 von den amerikanischen Mathematikern Ronald L. Rivest, Adi Shamir und Leonard Adleman vorgestellt. Nach den Anfangsbuchstaben ihrer Namen wird es als RSA-Verfahren bezeichnet. Eine mathematische Beschreibung asymmetrischer Verschlüsselungsverfahren kann hier aus Zeitgründen nicht geleistet werden. Es soll ausreichen, das Vorgehen beim
zu beschreiben. Bei anschaulichen Darstellungen kryptographischer Verfahren ist es weit verbreitet, Namen für die handelnden Parteien zu vergeben. Die Absenderin A einer Nachricht heißt üblicherweise Alice, der Empfänger B Bob und eine dritte, unerlaubt abhörende Partei E Eve (in Anlehnung an die englische Bezeichnung eavesdropper, was auf deutsch Lauscher(in) oder Horcher(in) bedeutet).
Will Alice an Bob eine verschlüsselte Nachricht übermitteln, dann geht sie unter der Voraussetzung, dass sie und Bob das gleiche Public-Key-System verwenden, folgendermaßen vor:
Falltürfunktionen, auf denen asymmetrische Verschlüsselungsverfahren beruhen, sind so beschaffen (ihr Name weist darauf hin), dass eine möglicherweise vorhandene Lauscherin Eve, die sowohl Bobs öffentlichen Schlüssel als auch den Geheimtext erfahren hat, daraus nicht in akzeptabler Zeit Bobs geheimen Schlüssel berechnen kann, den sie aber zum Entschlüsseln des Geheimtextes bräuchte.
Beim Erstellen einer digitalen Unterschrift unter ein wie auch immer geartetes Dokument ist das Vorgehen ein anderes als beim Verschlüsseln von Dokumenten und es wird zusätzlich eine der bereits vorgestellten Hashfunktionen eingesetzt. Angenommen, Alice will Bob ein (unverschlüsseltes) Dokument so zustellen, dass dieser feststellen kann, dass es tatsächlich von Alice stammt. Dazu muss Alice ihr Dokument um einen Zusatz ergänzen, der den gleichen Zweck hat, wie eine Unterschrift unter ein nicht digitales Dokument. Sie geht folgendermaßen vor, wobei eine kryptographische Hashfunktion und ein Public-Key-System vorgegeben und allen Beteiligten bekannt sind:
Eine Lauscherin Eve, die das Dokument D, die Signatur und den öffentlichen Schlüssel von Alice kennt, kann nichts ausrichten, weil ihr der geheime Schlüssel von Alice fehlt und sie diesen nicht in akzeptabler Zeit aus dem öffentlichen Schlüssel berechnen kann.
Beim Betrieb einer Blockchain wird von beiden Anwendungen asymmetrischer Verschlüsselungsverfahren Gebrauch gemacht. Durch digitale Signaturen werden die in der Blockchain aufzuzeichnenden Sachverhalte autorisiert und durch Verschlüsselung geschützt. Beispielsweise ist bei der Blockchain-Anwendung Bitcoin die Nummer eines Benutzkontos ein öffentlicher Schlüssel des Kontoinhabers. Mit ihm kann jeder, der die Kontonummer kennt, dem Kontoinhaber eine verschlüsselte Nachricht zukommen lassen, die nur dieser mit seinem privaten Schlüssel entschlüsseln kann.