SIC-1580 INSIGHTS



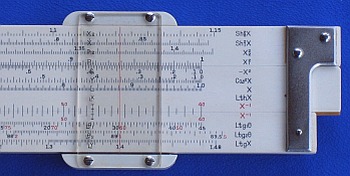
Why the P Y T H A G O R A S can be calculated with the P2, P1 & Q-Scales ???
******************************************************************************
c2 = a2 + b2
Starting with a scale of lenght 2p ...
0 1/4 1/2 3/4 1 1.25 1.5 1.75 2
|--------+--------+--------+--------+--------+--------+--------+--------|
Take the SQUAREROOT of this scale ...
0 0.5 0.707 0.866 1 1.118 1.225 1.323 1.414
|--------+--------+--------+--------+--------+--------+--------+--------|
|<=============== P1 ==============>|<=============== P2 ==============>|
|<=============== Q ===============>| P2 = sqrt( 1 + P12 )
1 0.866 0.707 0.5 0 Q = sqrt( 1 - P12 )
|--------+--------+--------+--------| = P1 inverted
Proof: P2 = sqrt( 1 + 0.52 ) = 1.118
====== sqrt( 1 + 0.7072 ) = 1.225
...
Q = sqrt( 1 - 0.52 ) = 0.866
sqrt( 1 - 0.7072 ) = 0.707
...
Now the scales P1, P2, & Q can be used for ADDING SQUARES ( see EX.A ) ...
========
a=0.4
0 v 0.5 0.707 0.866 1 1.118
|<====|--+--------+--------+--------+--------+---
|--------+--------+--------+-----|=>|
1 0.866 0.707 0.5 ^ 0 c2 = a2 + b2
b=0.3 0.52 = 0.42 + 0.32
The Hyperbolic Functions of the BACK SIDE, based on scales P1 & P2 ...
o have an extended domain and resolution
o AND use P2 for calculating CosH(X) directly
o AND calculate directly HYPERBOLIC FUNCTIONS OF COMPLEX QUANTITIES
Back to the SIC-1580 Main Page
Papers presented at the 3rd BERLIN-BRANDENBURGER SAMMLER-TREFFEN (BBST) in Berlin
impressum:
*********************************************************************************
© C.HAMANN http://public.BHT-Berlin.de/hamann 03/15/09
|