Zusammenfassung der Diplomarbeit von René Welzer WS 2003

Betreuerin: Prof. Dr. Angela Schwenk-Schellschmidt
Gutachter: Prof. Uwe Stephan

1. Grundlagen

Differentialgleichungen bieten eine vielfältige Möglichkeit von Anwendungen, z.B. in der Physik (Schwingungsvorgänge) oder in der Biologie (Wachstumsprozesse). Ein besonderer Typ von Differentialgleichungen sind die sog. "autonomen" Differentialgleichungen bzw. "autonomen" Differentialgleichungssysteme.

Definition:

f, g seien stetig partiell differenzierbare Funktionen auf einer offenen Menge G der (x, y)-Ebene. Das Differentialgleichungssystem (I) x' = f(x, y) y' = g(x, y) heißt autonomes Differentialgleichungssystem. Ein Paar von nach t differenzierbaren Funktionen (x(t), y(t)), die der Bedingung (II) x'(t) = f(x(t), y(t)) y'(t) = g(x(t), y(t)) genügen, heißt Lösung des autonomen Differentialgleichungssystems. Diese Beziehung sei auf I = (a, b) definiert.

Die Lösung des Differentialgleichungssystems (x und y) hängt nur von t ab. Die Funktionen f und g sind jedoch von t unabhängig. Dies ist für die nachfolgenden Betrachtungen bedeutend. Aufgrund dieser Autonomie (Unabhängigkeit) der Funktionen f und g von der Variablen t spricht man von einem "autonomen" Differentialgleichungssystem.

In dieser Arbeit werden ausschließlich "ebene" Systeme behandelt. Diese Bezeichnung hat sich für autonome Differentialgleichungssysteme mit zwei Gleichungen durchgesetzt, da die Lösungen (x(t), y(t)) als Kurven in der x-y-Ebene interpretiert werden können. Diese Kurven heißen Trajektorien. Aufgrund der Konstanten, die durch den Integrationsprozess entstehen, ergeben sich Trajektorienscharen die ein Phasenporträt bilden. Die Phasenporträts sind immer zusammen mit dem zugehörigen Vektorfeld abgebildet, da die Vektoren den Verlauf der Kurven für wachsendes t andeuten (vgl. Abb. 1).

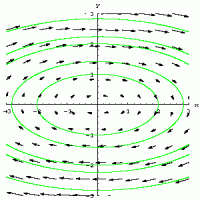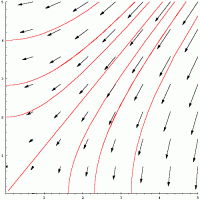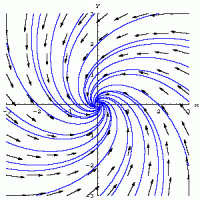
Abb. 1: Drei Phasenporträts mit dem Gleichgewichtspunkt (0, 0)

Eines der wichtigsten Gebiete in der Theorie über autonome Differentialgleichungen ist die Stabilitätstheorie. Hier wird untersucht, ob sog. Gleichgewichtspunkte stabil, asymptotisch stabil oder instabil sind. Ein Gleichgewichtspunkt (oder singuläre Lösung) ist eine Lösung des Differentialgleichungssystems, bei der die Bedingung x'(t) = f(x(t), y(t)) = 0, y'(t) = g(x(t), y(t)) = 0 für alle t erfüllt ist. An den folgenden beiden Bildern wird verdeutlicht, was mit stabil, asymptotisch stabil oder instabil gemeint ist, ohne die ausführliche und komplizierte Definition niederzuschreiben.

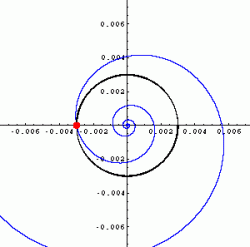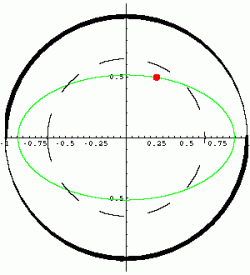
Abb. 2/Abb. 3

Zunächst wird die Abbildung 3, die Ellipse, betrachtet: Angenommen, die Kurven verlaufen für wachsende t gegen den Uhrzeigersinn und periodisch immer wieder auf Ellipsenbahnen. Dann lässt sich ein zu jedem ein finden, sodass zu einem Zeitpunkt t₁ (roter Punkt), die Trajektorie innerhalb des gestrichelten Kreises mit dem Radius liegt. Nun kann die Trajektorie durchaus noch mehrfach die -Umgebung verlassen, wird aber die -Umgebung (durchgezogener, dicker Kreis) des Gleichgewichtspunktes (0, 0) nie erreichen. Dieses Verhalten wird als "stabil" bezeichnet.

Nun zur Abbildung 2, der Spirale: Gegeben sei ein Kreis um den Ursprung mit Radius R. Angenommen, für wachsendes t verlaufe die Kurve in Richtung Ursprung. Dann lässt sich ein Zeitpunkt t₁ finden (roter Punkt), an dem die Spirale in den Kreis eindringt. Für t > t₁ gilt nun, dass für t die Lösung (x(t), y(t)) nach (0, 0) strebt ("die Trajektorie konvergiert gegen den Gleichgewichtspunkt"). Wenn eine Lösung stabil ist und darüber hinaus noch diese gerade eben beschriebene Eigenschaft besitzt, bezeichnet man den zughörigen Gleichgewichtspunkt "asymptotisch stabil".

Ein Gleichgewichtspunkt ist instabil, wenn er nicht stabil ist. Ein Beispiel dafür stellt die Spirale (Abb. 2) dar, sofern angenommen wird, dass sie sich für wachsendes t vom Ursprung entfernt.

Es zeigt sich, dass bei linearen Differentialgleichungssystemen der Form x' = Ax mit der konstanten Koeffizientenmatrix A der Stabilitätscharakter der Gleichgewichtspunkte nur von den Eigenwerten von A abhängt. Es ergeben sich folgende Resultate:

Gerade bei nicht-linearen Differentialgleichungssystemen ist das Bestimmen der Lösungskurven und anhand dieser dann das Bestimmen des Stabilitätsverhaltens sehr schwierig. Alexander Lyapunov (1857 - 1918; siehe Bild) entwickelte ein Verfahren, mit dessen Hilfe man, ohne vorher die Lösung zu bestimmen, Aussagen über das Stabilitätsverhalten der Gleichgewichtspunkte machen kann.

Definition:

(0, 0) sei isolierter Gleichgewichtspunkt des Systems (I) x' = f(x, y) y' = g(x, y). Die Funktion E(x, y) heißt Lyapunov-Funktion für das System, wenn sie in einer gewissen offenen Umgebung von (0, 0) die nachstehenden Eigenschaften besitzt: E ist stetig differenzierbar, d.h. die partiellen Ableitungen existieren und sind stetig. E verschwindet im Nullpunkt und ist außerhalb desselben größer als Null. verschwindet im Nullpunkt und ist außerhalb desselben kleiner oder gleich Null.

Bemerkung:
Zu Punkt 3 aus dieser Definition: Steht hier anstatt der Bedingung "kleiner oder gleich" die Bedingung "echt kleiner" als Null, so spricht man von einer "strengen Lyapunov-Funktion".

Lyapunov hat nun folgendes bewiesen:
Findet man solch eine (strenge) Funktion (später wurde sie dann "Lyapunov-Funktion" genannt), so ist (0, 0) (asymptotisch) stabil. Gilt bei Punkt 3 der Definition anstelle kleiner oder gleich Null größer als Null, so ist (0, 0) instabil.

2. Anwendung: Das LOTKA-VOLTERRAsche Räuber-Beute-Modell

Es beschreibt folgendes Szenario:

Es wird eine Räuberpopulation und eine Beutepopulation betrachtet. Die Größe der Beute-Population wird durch x(t), die der Räuber-Population mit y(t) beschrieben. Wir nehmen an, dass die Beutetiere einen unbegrenzten pflanzlichen Nahrungsvorrat haben. Die Räuber ernähren sich ausschließlich von den Beutetieren.

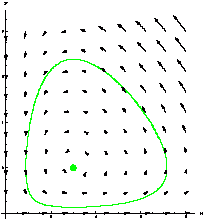Es zeigt sich, dass nie eine der beiden Populationen vollkommen ausstirbt, da sie von einander abhängen. Ernähren sich die Räuber von der Beute, so nimmt deren Anzahl ab und die der Räuber zu. Irgendwann ist aber nicht mehr genug Beute für die mittlerweile beachtliche Anzahl an Raubtieren. Diese verhungern in größerer Anzahl und der Bestand der Beutetiere kann sich erholen und steigt wieder an. Es handelt sich hierbei um einen immer wiederkehrenden (periodischen) Prozess. Das Differentialgleichungssystem besitzt zwei Gleichgewichtspunkte: (0, 0) und (c/d, a/b). (0, 0) beschreibt den Zustand, dass keine der beiden Populationen existiert, er ist also relativ uninteressant. Das sich ergebende Phasenporträt (siehe Abbildung) verdeutlicht sehr schön, dass es sich um einen periodischen Prozess handelt. Der eingetragen Punkt ist der Gleichgewichtspunkt (c/d, a/b).

3. Besonderheiten ebener autonomer Differentialgleichungssysteme

Da sich diese Arbeit ausschließlich mit ebenen autonomen Differentialgleichungssystemen beschäftigt, gehe ich noch auf ein paar Besonderheiten dieser Systeme ein.

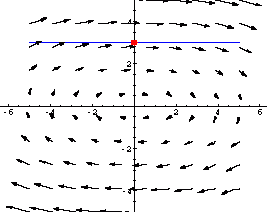Zu einem Phasenporträt eines ebenen autonomen Differentialgleichungssystems bzw. zu den Trajektorien dieses Systems lässt sich eine sogenannte "Transversale" finden. Eine Transversale ist eine beidseitig offene Teilstrecke einer Geraden. Auf ihr liegen die Vektoren des Vektorfeldes , die nicht gleich dem Nullvektor sind und nicht parallel zur Geraden verlaufen.

In dem in der Abbildung gewählten Beispiel wurde die Gerade mit der Gleichung und das Vektorfeld gewählt. Bis auf die rot markierte Stelle ist die blaue Gerade Transversale. Es lässt sich zeigen, dass in bestimmten Intervallen die Trajektorien die Transversale immer nur in eine Richtung durchsetzen. Dieser Tatsache bedienen sich viele Sätze in der Theorie über Transversalen.

Eine besondere Rolle bei der Theorie über Differentialgleichungssysteme spielen periodische Lösungen. Wichtige Vorgänge in der Natur, z.B. die ungedämpfte Schwingung oder das Räuber-Beute-Modell, sind periodisch und lassen sich durch Differentialgleichungen beschreiben. Die Theorie von Poincaré-Bendixson stellt hier einen Meilenstein dar. Sie bewiesen den folgenden

Satz:

Der kompakte Bereich B der xy-Ebene möge keine Gleichgewichtspunkte des Differentialgleichungssystems x' = f(x, y) y' = g(x, y) enthalten, und T0 :={(x(t), y(t))} sei eine Trajektorie dieses Systems, die für alle t > t0 in B verläuft. Dann ist T entweder selbst ein Zyklus oder schmiegt sich für t spiralförmig von innen oder außen einem Zyklus aus B an. Kurz: Wenn B eine Halbtrajektorie enthält, so gibt es in B gewiss auch einen Zyklus.

An der folgenden Zeichnung lässt sich sehr schön die Bedeutung dieses Satzes veranschaulichen.

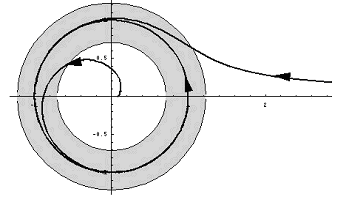
Der Bereich B sei die graue Fläche in der Zeichnung. Es wird deutlich, dass eine Trajektorie T, die einmal B erreicht, diesen Bereich nicht mehr verlässt. Oder anders ausgedrückt: Die Halbtrajektorie T⁺ läuft ab einem bestimmten t > t₀ ganz in B.

Letzte Änderung am 12.01.2004