Prof. Dr. Angela Schwenk

Die erzwungene Schwingung - Resonanzkurven im Vergleich

Die erzwungene Schwingung wird durch die inhomogene Schwingungsgleichung    y" + 2betay ' + omega02 y = g(t)    beschrieben. Dabei ist die Störfunktion g(t) durch die äußere periodische Anregung gegeben.

Nach dem Einschwingvorgang ergibt sich die stationäre Lösung (Partikulärlösung) als harmonische Schwingung, deren Kreisfrequenz mit der Erregerkreisfrequenz omega übereinstimmt und deren Amplitude von der Erregerfrequenz omega und der Dämpfung beta abhängt. Die Resonanzkurven in den Abbildungen unten zeigen die Amplitude als Funktion der Erregerkreisfrequenz omega für verschiedenen Dämpfungen beta. Die Dämpfung variiert dabei von beta=0 (rot) bis beta=10omega0 (blau).

mechanische Schwingung
y" + 2betay ' + omega02 y = F0cos(omegat)


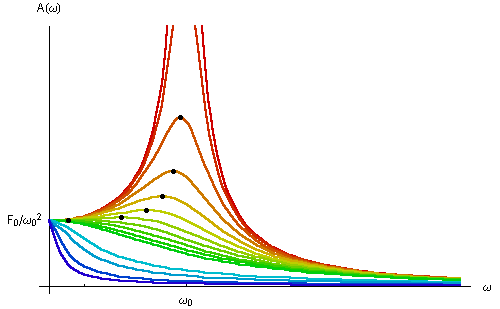
Die Maxima der Resonanzkurven hängen von der Dämpfung ab. Für die zugehörigen Resonanzfrequenzen gilt . Resonanzmaxima gibt es nur für kleine Dämpfungen mit .
elektr. Schwingung
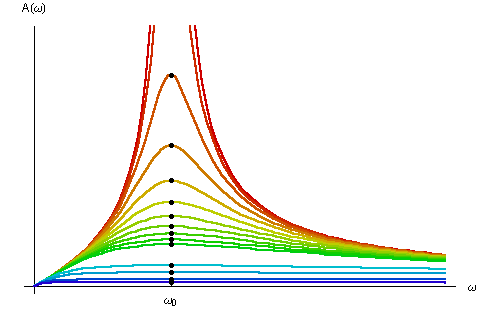
y" + 2betay ' + omega02 y = omegaF0cos(omegat)


Beim elektromagnetischen Reihenschwingkreis ergibt sich eine Störfunktion, die im Vergleich zur mechanischen Schwingung mit omega multipliziert ist. Damit enthält auch die Amplitudenfunktion A(omega) den Faktor omega. Als Konsequenz hängt die Resonanzfrequenz nicht von der Dämpfung ab, es gilt stets omegaR = omega0 unabhängig von der Dämpfung beta.
 <- Schwingungsgleichungen - Übersicht             <- Weitere Bilder      <- Home Page Mathematik

Letzte Änderung am: 01.04.2009