Prof. Dr. Angela Schwenk
    Springbrunnen - klicken zur Vergrößerung mit Parabel
    Orientalischer Garten im Erholungspark Marzahn, [Vergrößerung mit Parabel]

    Wurfparabeln - Springbrunnen

    Abbildung 1 zeigt Momentanbilder eines Balles, die jeweils nach gleichen Zeitabständen aufgenommen wurden.

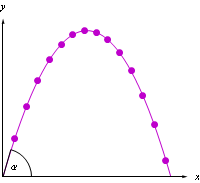
    Bahnkurve eines Balles, schiefer Wurf
    Abb. 1: Bahnkurve eines Balles, schiefer Wurf

    Die Punktkoordinaten des Balles hängen von der Zeit t ab. Die Bahnkurve des schiefen Wurfs (ohne Reibung) lautet:

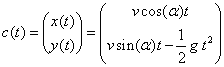    Gleichung der Bahnkurve ,
    dabei sind v die Abwurfgeschwindigkeit, α der Abwurfwinkel zur Horizontalen und g die Erdbeschleunigung. Variiert man den Abwurfswinkel α bei unveränderter Anfangsgeschwindigkeit v, erhält man einen virtuellen Springbrunnen wie in Abbildung 2.

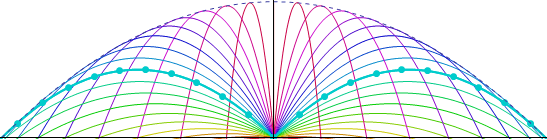
    Parabelschar - virtueller Sprinbrunnen
    Abb. 2: Virtueller Springbrunnen

    Die Bahnkurve, die zum Winkel 45° gehört, ist in Abbildung 2 durch die Momentanbilder hervorgehoben. Mit einem Abwurfswinkel von 45° wirft man weitesten, wenn das Aufschlagsniveau mit dem Abwurfsniveau übereinstimmt. Die Suche nach dem jeweils weitesten Wurf für andere Aufschlagsniveaus führt zur Einhüllenden der Schar der Wurfparabeln. Die Einhüllende dieser Wurfparabeln ist selbst auch eine Parabel. Sie hat die Gleichung

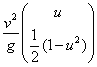    Parametrisierung der Einhüllenden ,
    dabei ist u=cot(α)

    Bei einem Springbrunnen markiert die einhüllende Parabel die Grenze der Bereiche, in denen man trocken bleibt bzw. nass wird. Man erkennt anhand der Gleichung, dass die Form der Einhüllenden unabhängig von der jeweils gewählten Anfangsgeschwindigkeit v ist. Der Faktor v^2/g bewirkt lediglich eine Größenänderung ohne Verzerrung, d. h. alle Springbrunnen, bei denen aus jeder Düse Wasser mit der gleichen Geschwindigkeit v austritt, haben die gleiche Form.



    Weitere Bilder     

    Letzte Änderung am: 28.07.2011